betareg

Diagnostic Plots for betareg Objects

Description

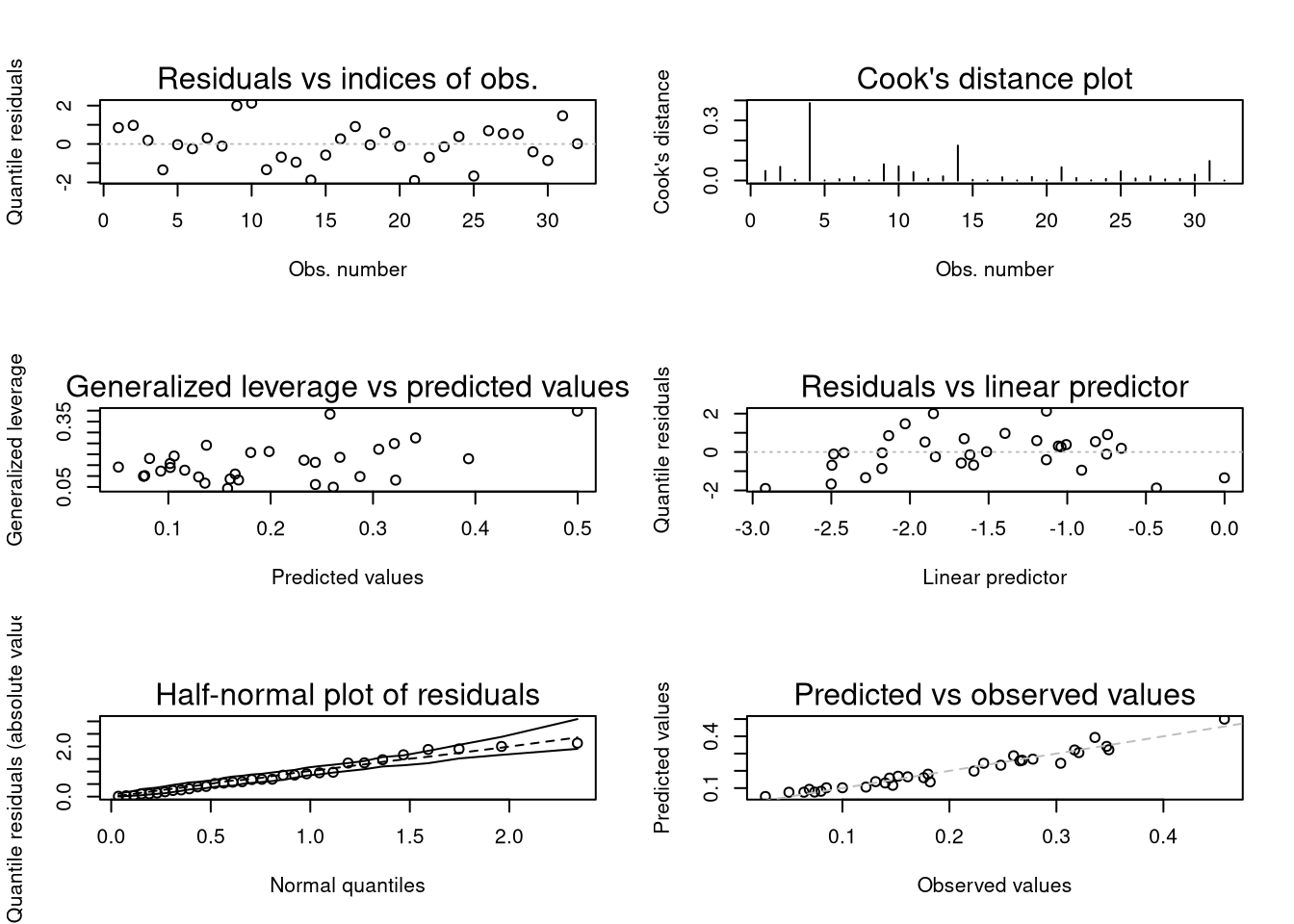
Various types of standard diagnostic plots can be produced, involving various types of residuals, influence measures etc.

Usage

## S3 method for class 'betareg'
plot(x, which = 1:4,
  caption = c("Residuals vs indices of obs.", "Cook's distance plot",
    "Generalized leverage vs predicted values", "Residuals vs linear predictor", 
    "Half-normal plot of residuals", "Predicted vs observed values"),
    sub.caption = paste(deparse(x\$call), collapse = "\n"), main = "", 
    ask = prod(par("mfcol")) < length(which) && dev.interactive(), 
    ..., type = "quantile", nsim = 100, level = 0.9)

Arguments

`x`	fitted model object of class `“betareg”`.
`which`	numeric. If a subset of the plots is required, specify a subset of the numbers `1:6`.
`caption`	character. Captions to appear above the plots.
`sub.caption`	character. Common title-above figures if there are multiple.
`main`	character. Title to each plot in addition to the above `caption`.
`ask`	logical. If `TRUE`, the user is asked before each plot.
`…`	other parameters to be passed through to plotting functions.
`type`	character indicating type of residual to be used, see `residuals.betareg`.
`nsim`	numeric. Number of simulations in half-normal plots.
`level`	numeric. Confidence level in half-normal plots.

Details

The plot method for betareg objects produces various types of diagnostic plots. Most of these are standard for regression models and involve various types of residuals, influence measures etc. See Ferrari and Cribari-Neto (2004) for a discussion of some of these displays.

The which argument can be used to select a subset of currently six supported types of displays. The corresponding element of caption contains a brief description. In some more detail, the displays are: Residuals (as selected by type) vs indices of observations (which = 1). Cook’s distances vs indices of observations (which = 2). Generalized leverage vs predicted values (which = 3). Residuals vs linear predictor (which = 4). Half-normal plot of residuals (which = 5), which is obtained using a simulation approach. Predicted vs observed values (which = 6).

References

Cribari-Neto F, Zeileis A (2010). Beta Regression in R. Journal of Statistical Software, 34(2), 1–24. doi:10.18637/jss.v034.i02

Ferrari SLP, Cribari-Neto F (2004). Beta Regression for Modeling Rates and Proportions. Journal of Applied Statistics, 31(7), 799–815.

Examples

library("betareg")

data("GasolineYield", package = "betareg")

gy <- betareg(yield ~ gravity + pressure + temp10 + temp, data = GasolineYield)

par(mfrow = c(3, 2))
plot(gy, which = 1:6)

par(mfrow = c(1, 1))