install.packages("topmodels", repos = "https://R-Forge.R-project.org")topmodels: Infrastructure for Inference and Forecasting in Probabilistic Models
1 Overview
Probabilistic predictions have been receiving increasing interest in various application fields over the last decades due to necessary functional risk management and strategy. Consequently, there is an increasing demand for appropriate probabilistic models and corresponding evaluations of the goodness of fit. Besides proper probabilistic scores (Gneiting and Raftery 2007), which evaluate not only the expectation but the entire predictive distribution, graphical assessment methods are particularly advantageous to diagnose possible model misspecification problems.
Probabilistic predictions are often based on distributional regression models, for which a wide range of different packages is readily available: from basic models like lm() and glm() in base R (which can be interpreted as probabilistic models and not just mean regression models), over general packages for distributional regression like gamlss (Stasinopoulos and Rigby 2007) or bamlss Umlauf et al. (2021) to more specific packages for certain purposes. Examples for the latter include pscl or countreg (Zeileis, Kleiber, and Jackman 2008) for count regression, crch (Messner, Mayr, and Zeileis 2016) for certain censored regression models, or betareg (Cribari-Neto and Zeileis 2010) for beta regression, among many others. However, there is no unified and object-oriented approach available for all these different models/packages that allows to compute predictive distributions, probabilities, and quantiles. Therefore, routines to evaluate probabilistic models either graphically or via scoring rules are not always available or may be specific to certain packages. An easy-to-use unified infrastructure for graphically assessing and comparing different probabilistic models is not available, yet.
The topmodels package is designed to fill this gap and provide such an unifiying infrastructure to obtain predictions of probabilities, densities, etc. for probabilistic models. The unifying prediction infrastructure is the basis for numerous graphical evaluation tools, such as rootograms (Kleiber and Zeileis 2016), PIT histograms (Gneiting, Balabdaoui, and Raftery 2007), reliagrams (reliability diagrams, Wilks 2011), randomized quantile Q-Q plots (Dunn and Smyth 1996), and worm plots (Buuren and Fredriks 2001).
To be able to use the object-oriented framework of topmodels, solely a procast() method must exist for the model class of interest. Currently the package provides generic procast methods for the model classes lm, glm, crch (Messner, Mayr, and Zeileis 2016), and disttree (Schlosser et al. 2019).
2 Installation
For the package topmodels so far only a development version is available, which is hosted on R-Forge at https://R-Forge.R-project.org/projects/topmodels/ in a Subversion (SVN) repository. The package can be installed via
or via
remotes::install_svn("svn://R-Forge.R-project.org/svnroot/topmodels/pkg/topmodels")where a specific revision can be installed by setting the optional argument revision.
3 Usage
The package topmodels provides various routines to easily graphically assess and compare different probabilistic models and model types using ggplot2 (Wickham 2016) and base R graphics:
library("topmodels")
m <- lm(dist ~ speed, data = cars)rootogram(m)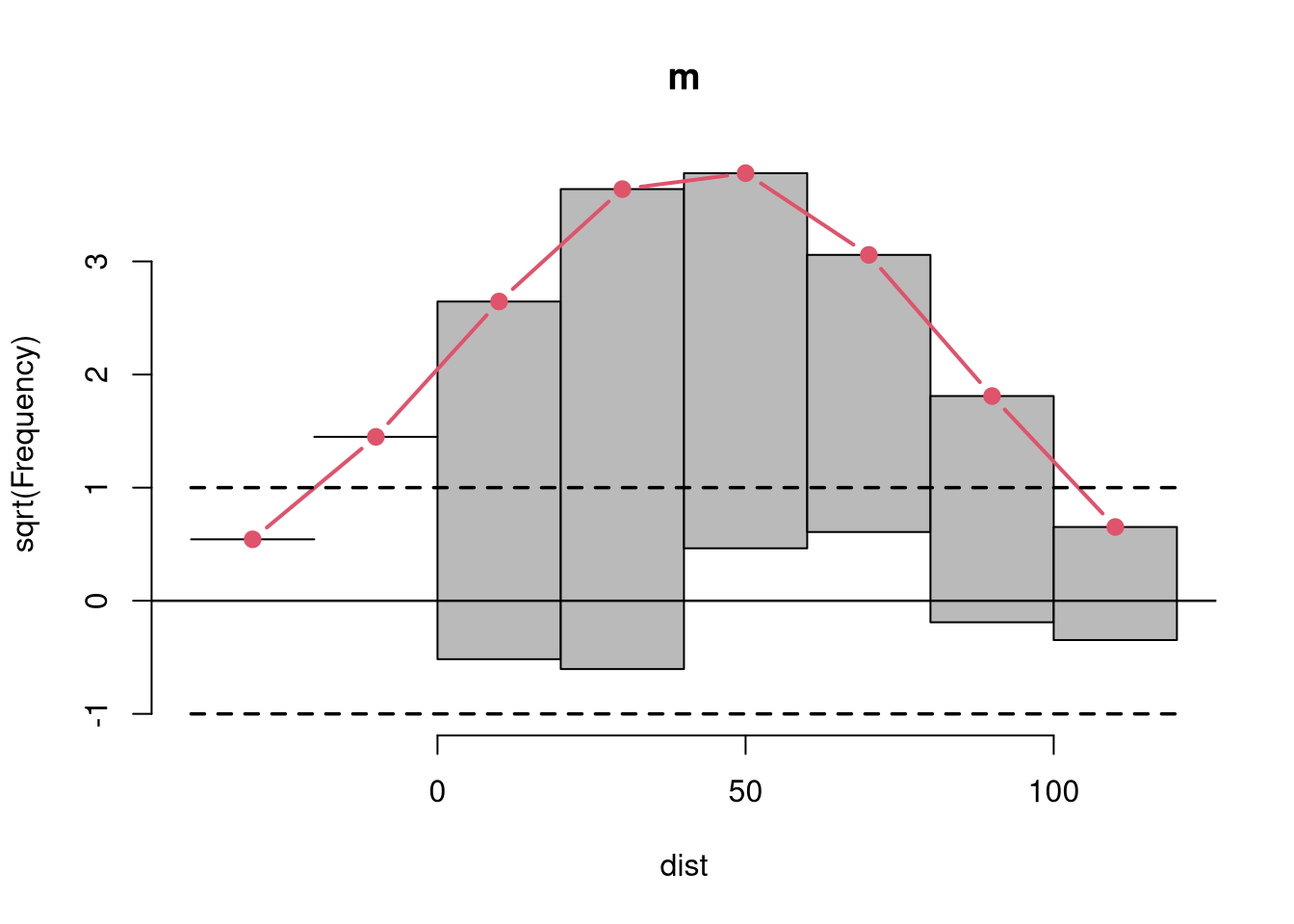
pithist(m)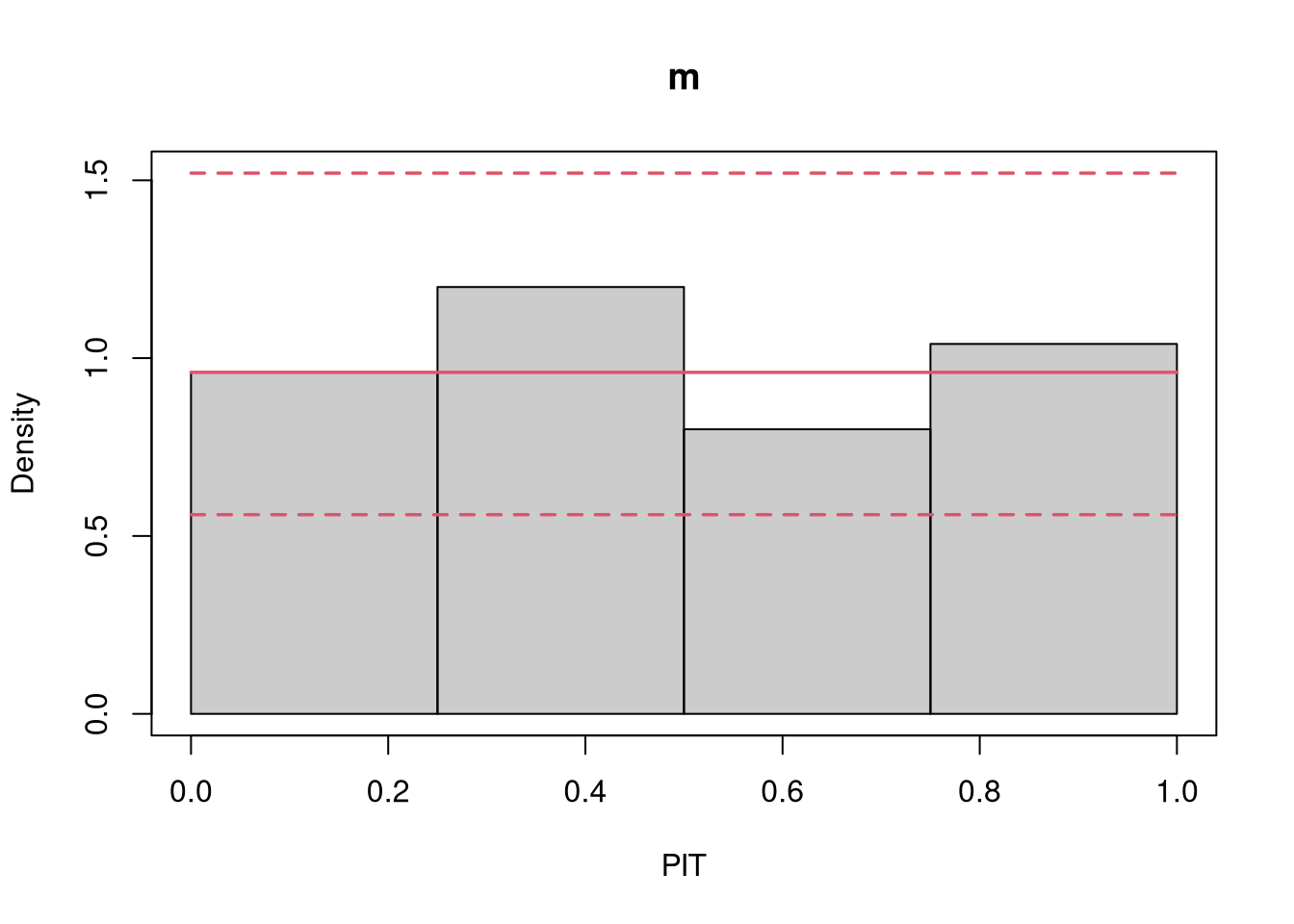
qqrplot(m)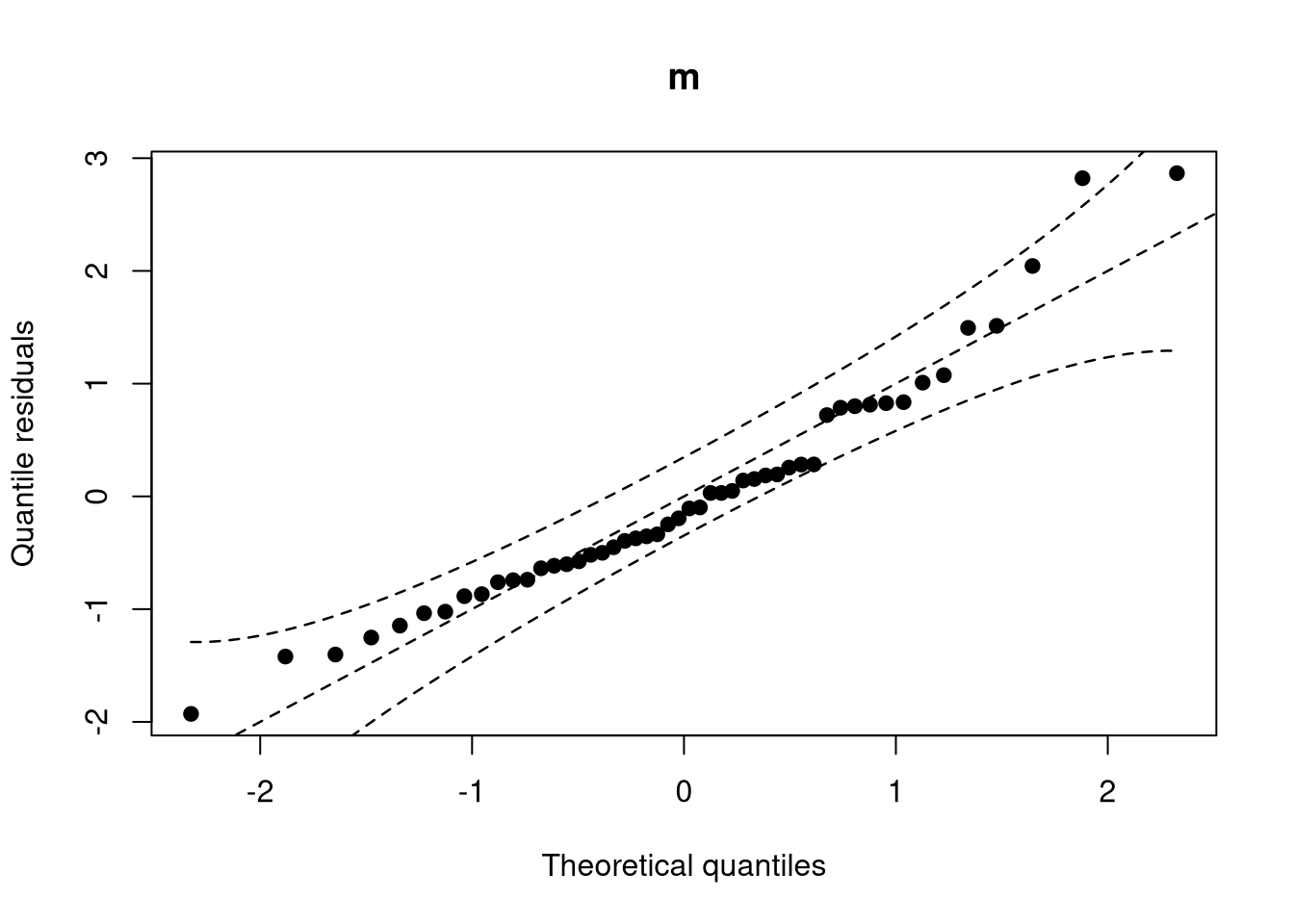
wormplot(m)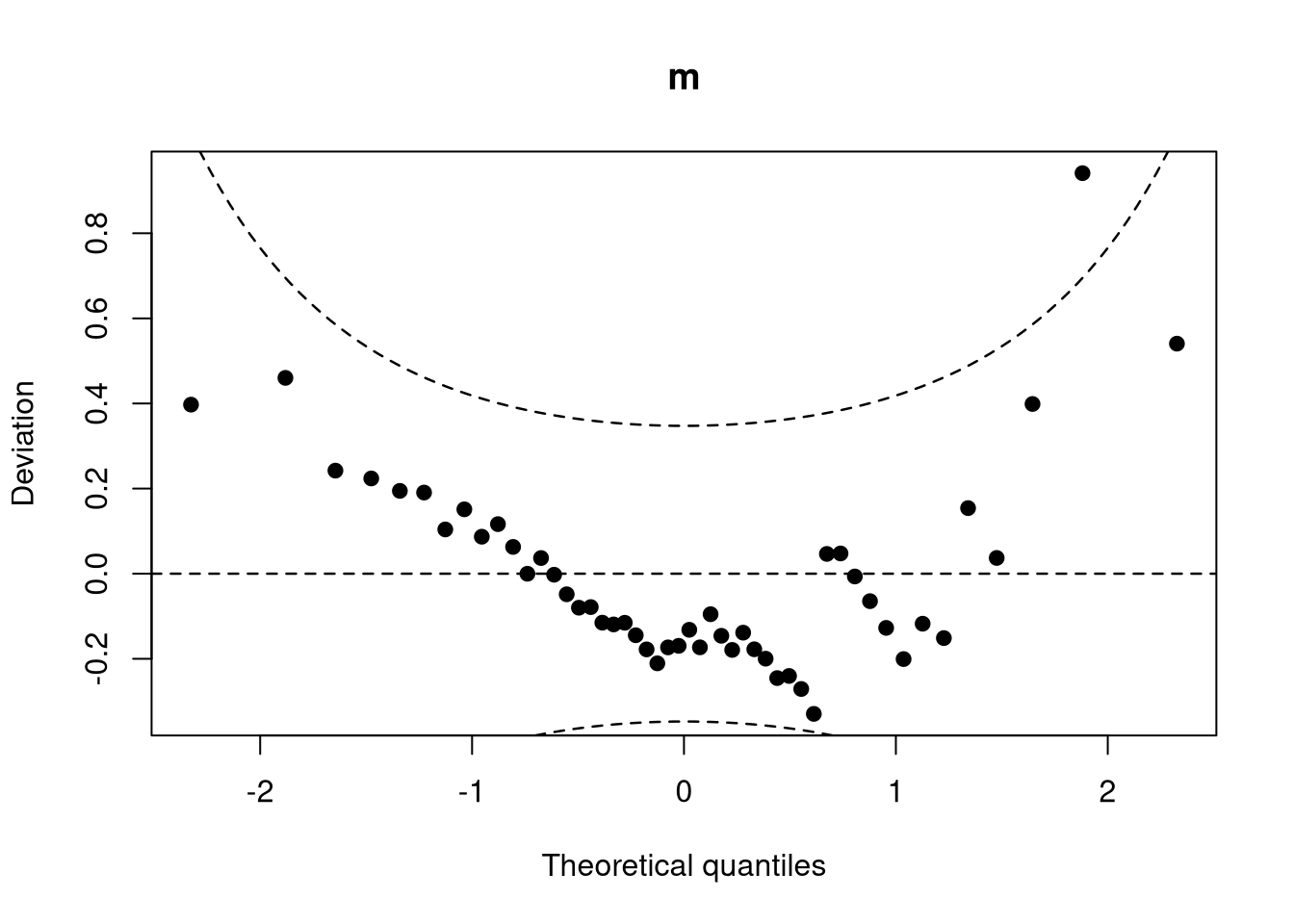
reliagram(m)