Warning in qqrplot_plot(x[x$group == i, ], ...): infinite sample quantile
drawn; limited to +/- 100 for plotting
Warning in qqrplot_plot(x[x$group == i, ], ...): infinite sample quantile
drawn; limited to +/- 100 for plotting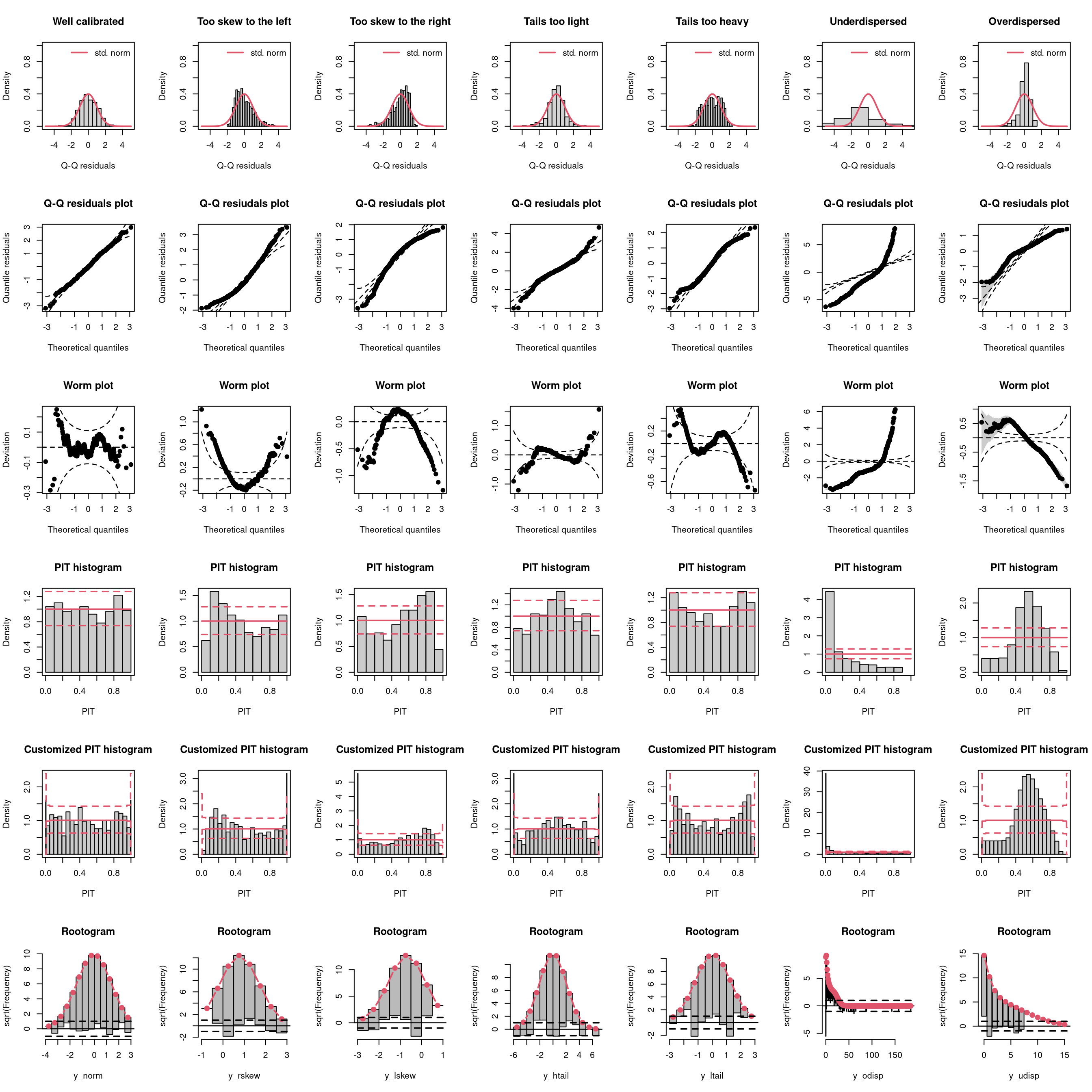
Warning in qqrplot_plot(x[x$group == i, ], ...): infinite sample quantile
drawn; limited to +/- 100 for plotting
Warning in qqrplot_plot(x[x$group == i, ], ...): infinite sample quantile
drawn; limited to +/- 100 for plotting
| Predictive distribution | well calibrated | too skew to the left | too skew to the right | tails too light | tails too heavy | underdispersed (underestimated variance) | overdispersed (overestimated variance) |
|---|---|---|---|---|---|---|---|
| Resdiuals | normal | right skewed | left skewed | heavy tailed | light tailed | overdispersed | underdispersed |
| Q-Q plot | bisecting line | positive curvature (bends up the line at both ends) | negative curvature (bends down at both ends) | reverse S-shape (dips below the line at the low end and rises above it at the high end) | S-shape | crossing qqline from below (?) | crossing qqline from above ? |
| Worm plot | horizontal line | U-shape | inverse U-shape | S-shape on the left bent down | S-shape on the left bent up | positive slope | negative slope |
| PIT histogram | uniform | skewed | skewed | superimposed U-shape | superimposed inverse U-shape” | U-shape | inverse U-shape |
| Rootogram | no deviations | ? | ? | wave-like (underfitting in the tails and the center) | ? | ? | ? |
| Interpretation | no misspecifications | ? | ? | values more extrem as expected | values less extrem as expected | ? | ? |
The following artificial data sets are simulated, with response values always depending on regressor variables, in order to obtain a realistic scenario for regression models:
make_residuals_plot <- function(object, breaks = breaks) {
name <- deparse(substitute(object))
set.seed(1)
pithist(object, breaks = c(0, 0.01, 1:9 / 10, 0.99, 1), main = name)
set.seed(1)
hist(qq <- proresiduals(object), freq = FALSE,
main = sprintf("Histogram of proresiduals(%s)", name), xlab = "Q-Q residuals")
curve(dnorm, from = min(qq), to = max(qq), col = 2, add = TRUE)
legend("topright", "std. norm", lty = 1, col = 2, bty = "n")
set.seed(1)
boxplot(data.frame("Q-Q residuals" = proresiduals(object), "std. norm" = rnorm(length(proresiduals(object)))))
}
make_topmodels_plot <- function(object) {
topmodels(object, which = c(1:2, 4:5), ask = FALSE, spar = FALSE)
}
set.seed(0)
## regressors
d <- data.frame(
x = runif(500, -1, 1),
z = runif(500, -1, 1)
)
## parameters
d <- transform(d,
lambda = exp(1 + 0.5 * x),
theta = 2,
mu = 50 + 22 * x,
sigma = 22,
sigmaz = exp(3 + 1 * z)
)
## responses
d <- transform(d,
ynorm = rnorm(500, mean = mu, sd = sigma),
yhnorm = rnorm(500, mean = mu, sd = sigmaz),
ytnorm = crch::rtnorm(500, mean = mu, sd = sigma, left = 0),
ycnorm = crch::rcnorm(500, mean = mu, sd = sigma, left = 0, right = 100),
yt = mu + sigma * rt(500, df = 4),
ylaplace = mu + rmutil::rlaplace(500, s = sigma),
yrskew = sn::rsn(500, xi = mu, omega = sigma, alpha = 5, tau = 0),
ylskew = sn::rsn(500, xi = mu, omega = sigma, alpha = -5, tau = 0),
yunif = mu + sigma * runif(500, min = -1, max = 1),
ypois = rpois(500, lambda = lambda),
ynegbin = rnbinom(500, mu = lambda, size = theta),
yzip = ifelse(runif(500) < 0.25, 0, rpois(500, lambda = lambda))
)As a reference, a linear normal model is fitted to simulated normally distributed data without conditional heteroscedasticity.
## correct model fit
m1 <- lm(ynorm ~ x, data = d)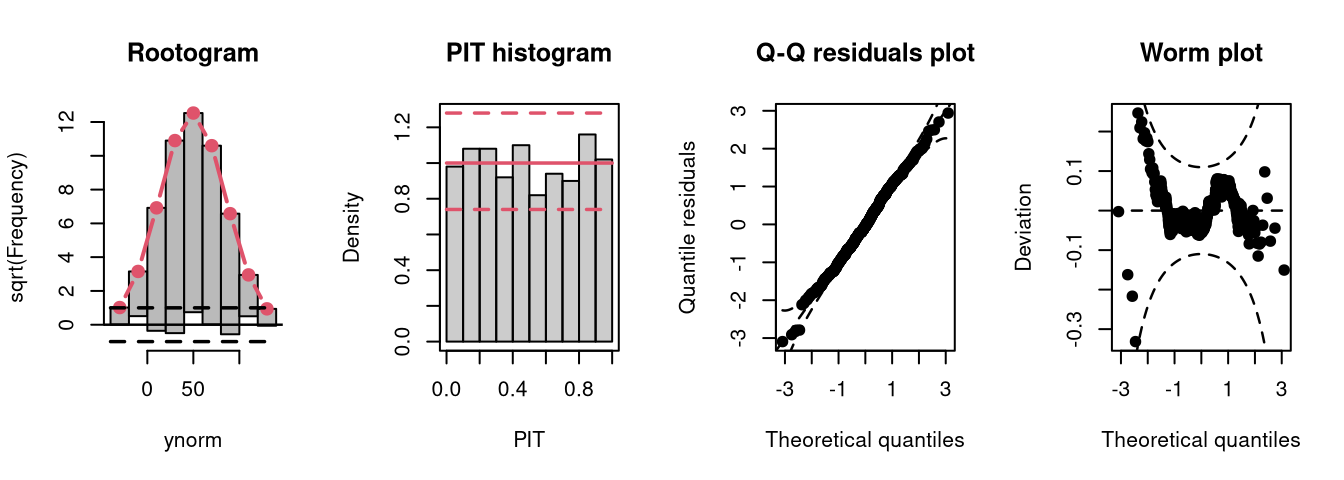
The model fit experiences no misspecifications resulting in a well calibrated predictive distribution (compare the case “well calibrated” in the summary plot of Graphical Evaluation: Methodology):
In the “conditional heteroscedasticity” example, two models are fitted to simulated data from the normal distribution where both the location and scale parameters depend on a regressor. The model m2 estimated with lm() cannot account for conditional heteroscedasticity, unlike the model m3 which is fitted with crch().
## not accounting for heteroscedasticity
m2 <- lm(yhnorm ~ x, data = d)
### accounting for heteroscedasticity
m3 <- crch(yhnorm ~ x | z, data = d)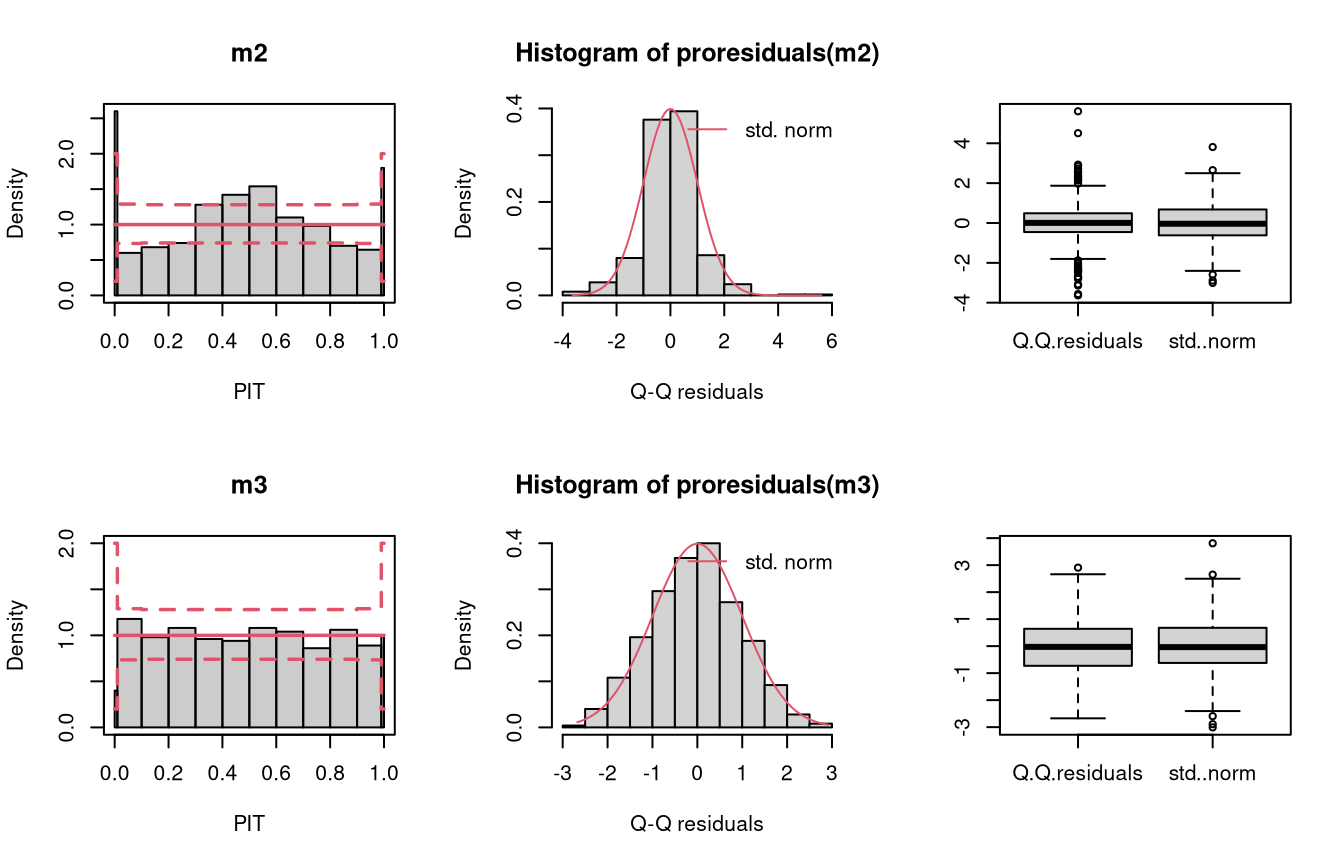
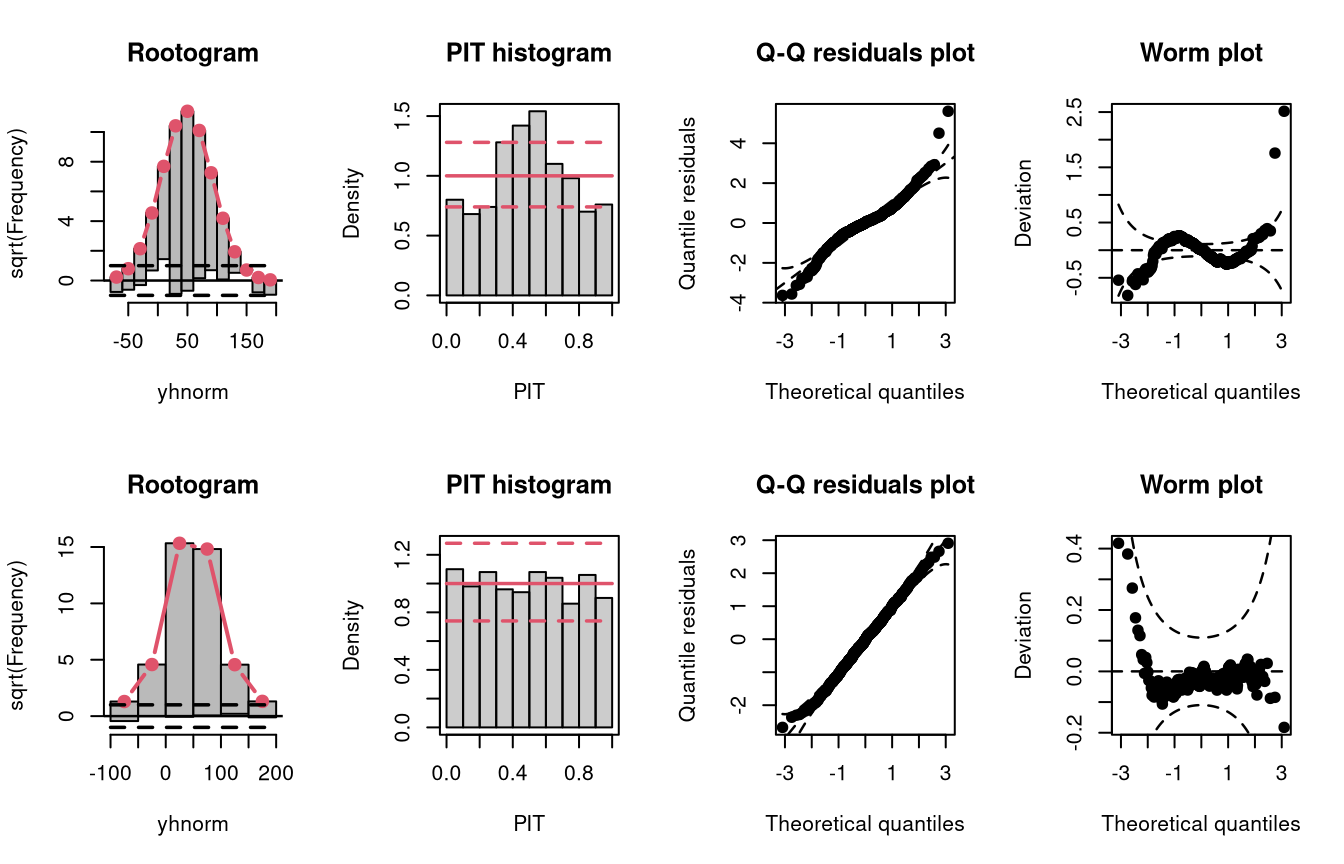
Not accounting for conditional heteroscedasticity results here in a model fit where the tails of the distribution are too light (compare the case “tails too light” in the summary plot of Graphical Evaluation: Methodology):
To investigate the graphical evaluation tools under the misspecification of not accounting for censoring in the estimation, homoscedastic normally distributed data are simulated with censoring at 0 and 100. The model m4 fitted with lm() cannot account for the censored data, contrary to the model m5 estimated with crch().
## not accounting for censoring
m4 <- lm(ycnorm ~ x, data = d)
## accounting for censoring
m5 <- crch(ycnorm ~ x | 1, data = d, left = 0, right = 100)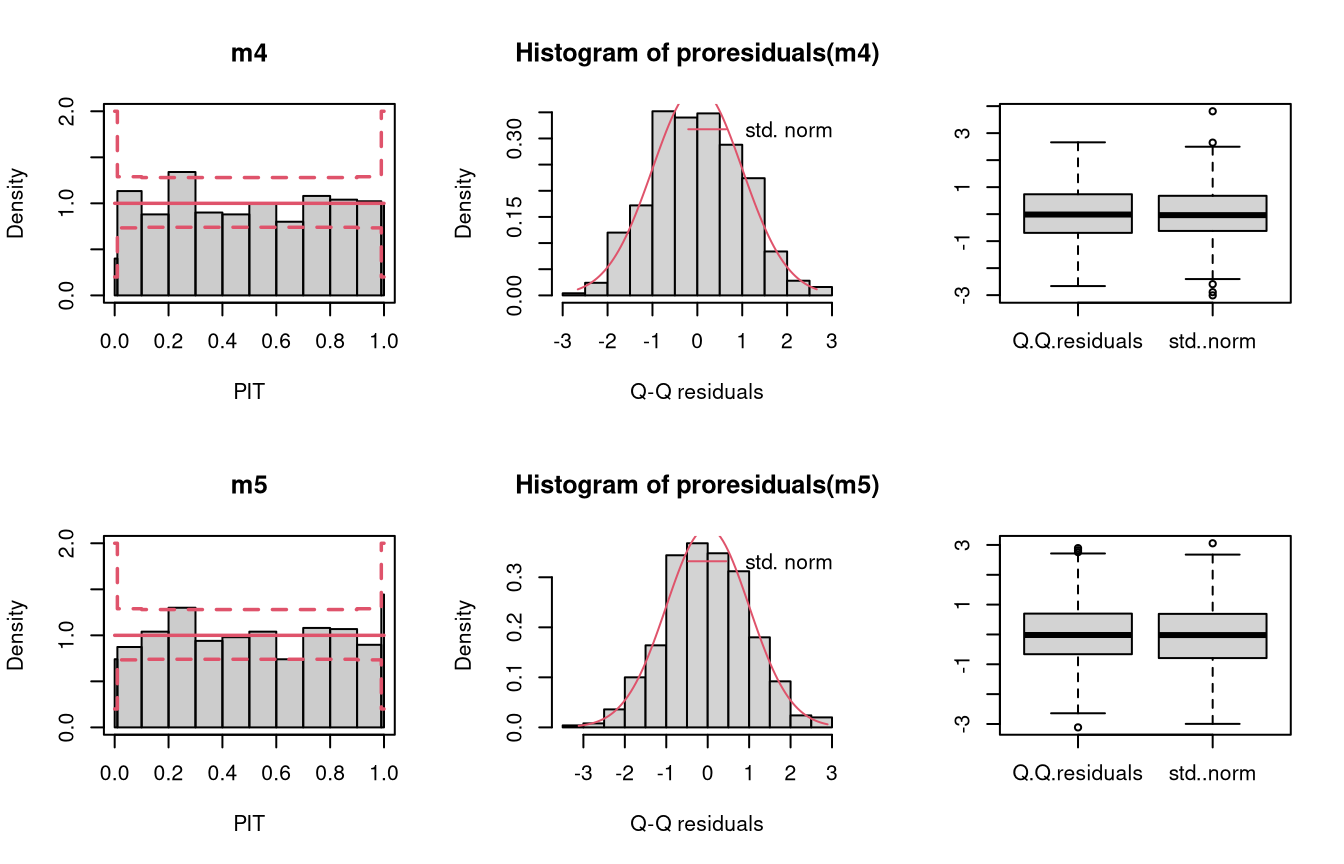
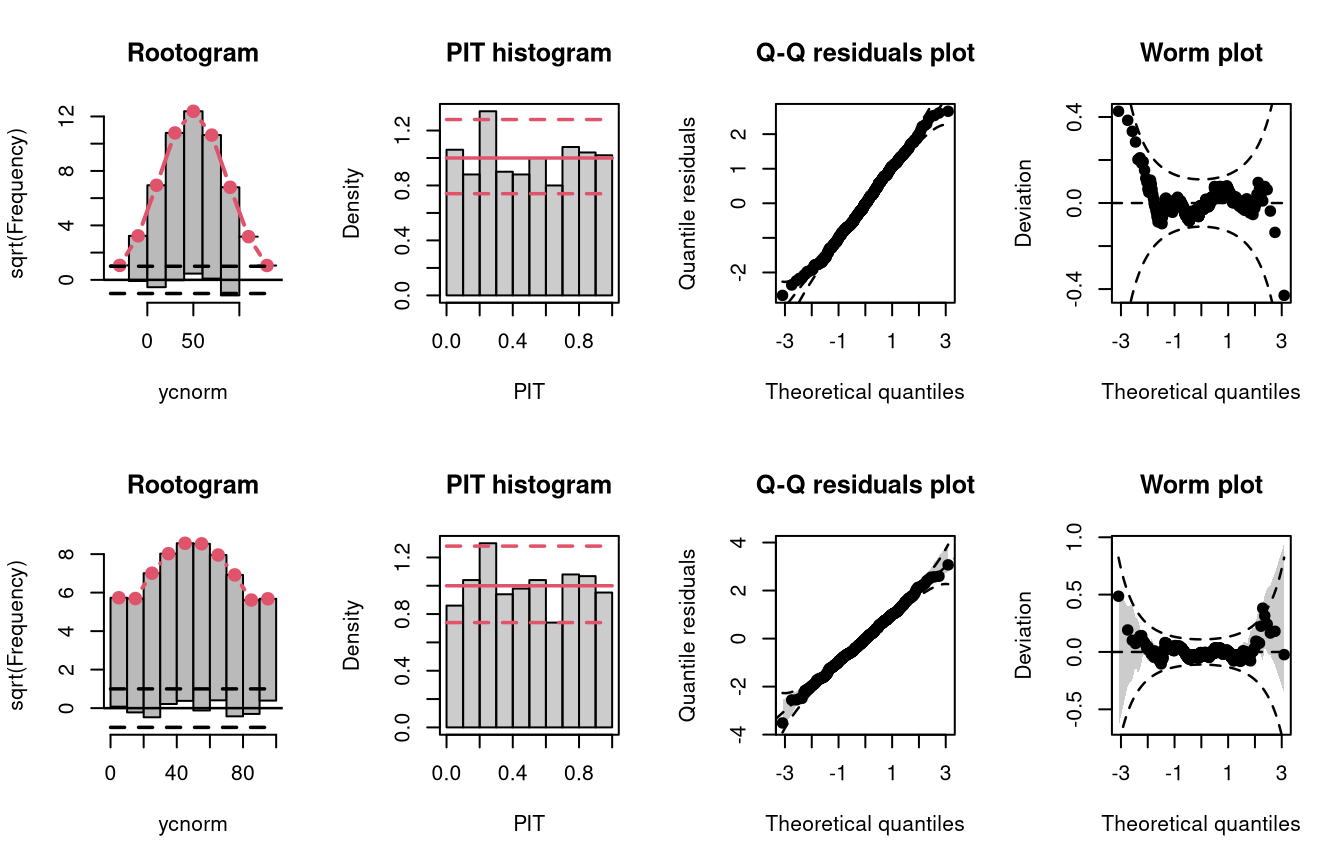
Not accounting for the censoring at 0 and 100 leads to an incorrect distributional assumption in the tails of the predictive distribution, similar to the case “tails too heavy” discussed in Graphical Evaluation: Methodology:
Here, the homoscedastic normally distributed response values are truncated at zero. The model m6 fitted with lm() cannot account correctly for this, contrary to the model m7 estimated with crch().
## not accounting for truncation
m6 <- lm(ytnorm ~ x, data = d)
# not accounting for truncation
m7 <- trch(ytnorm ~ x | 1, data = d, left = 0)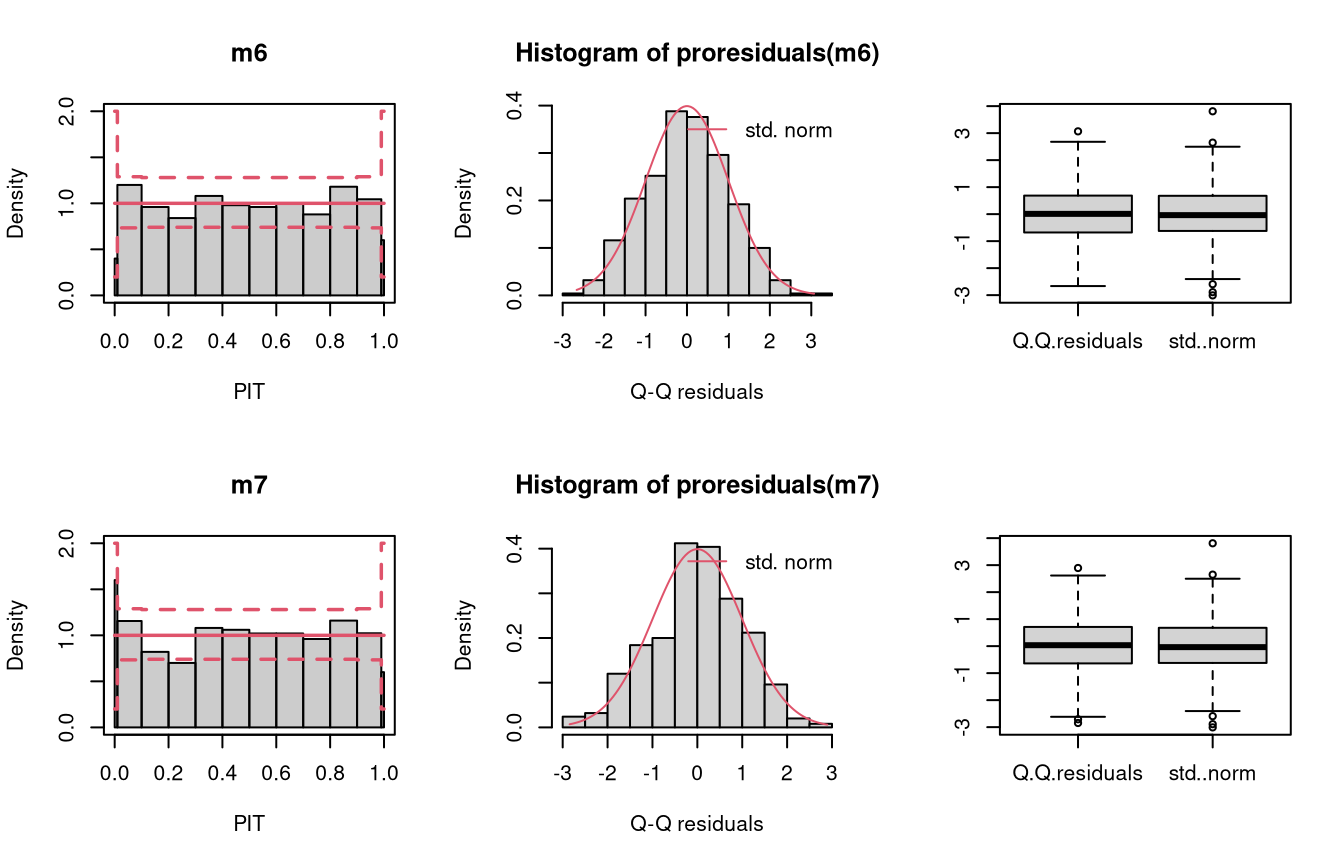
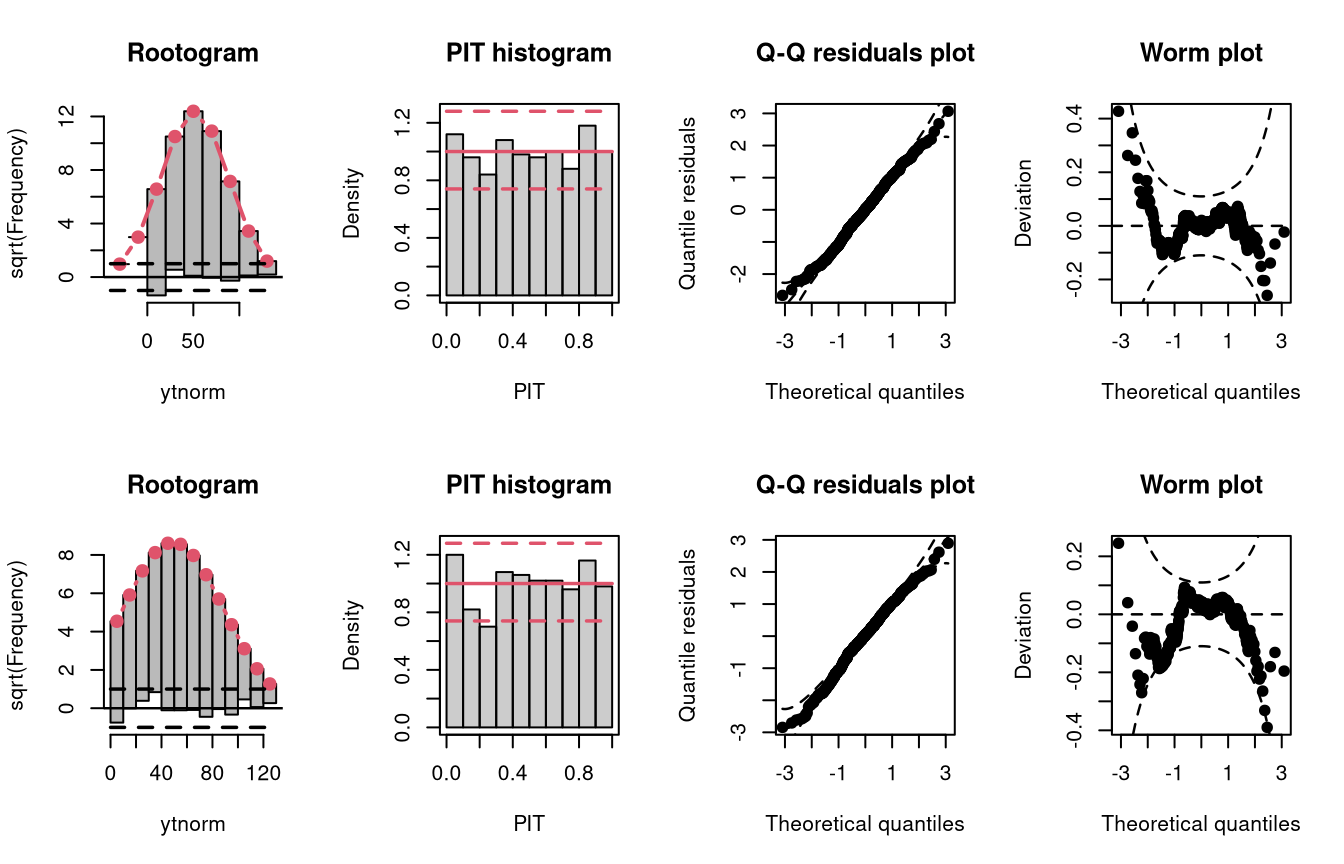
Not accounting for the truncation at 0 leads to an incorrect distributional assumption in the lower tail of the predictive distribution:
df = 4)In the following example, data is simulated from the student-t distribution with 4 degrees of freedom. The model m8 incorrectly assumes normally distributed data, while the model m9 correctly incorporates t-distributed data.
## not accounting for t_4 distributed data
m8 <- lm(yt ~ x, data = d)
## accounting for t_4 distributed data
m9 <- crch(yt ~ x | 1, data = d, dist = "student")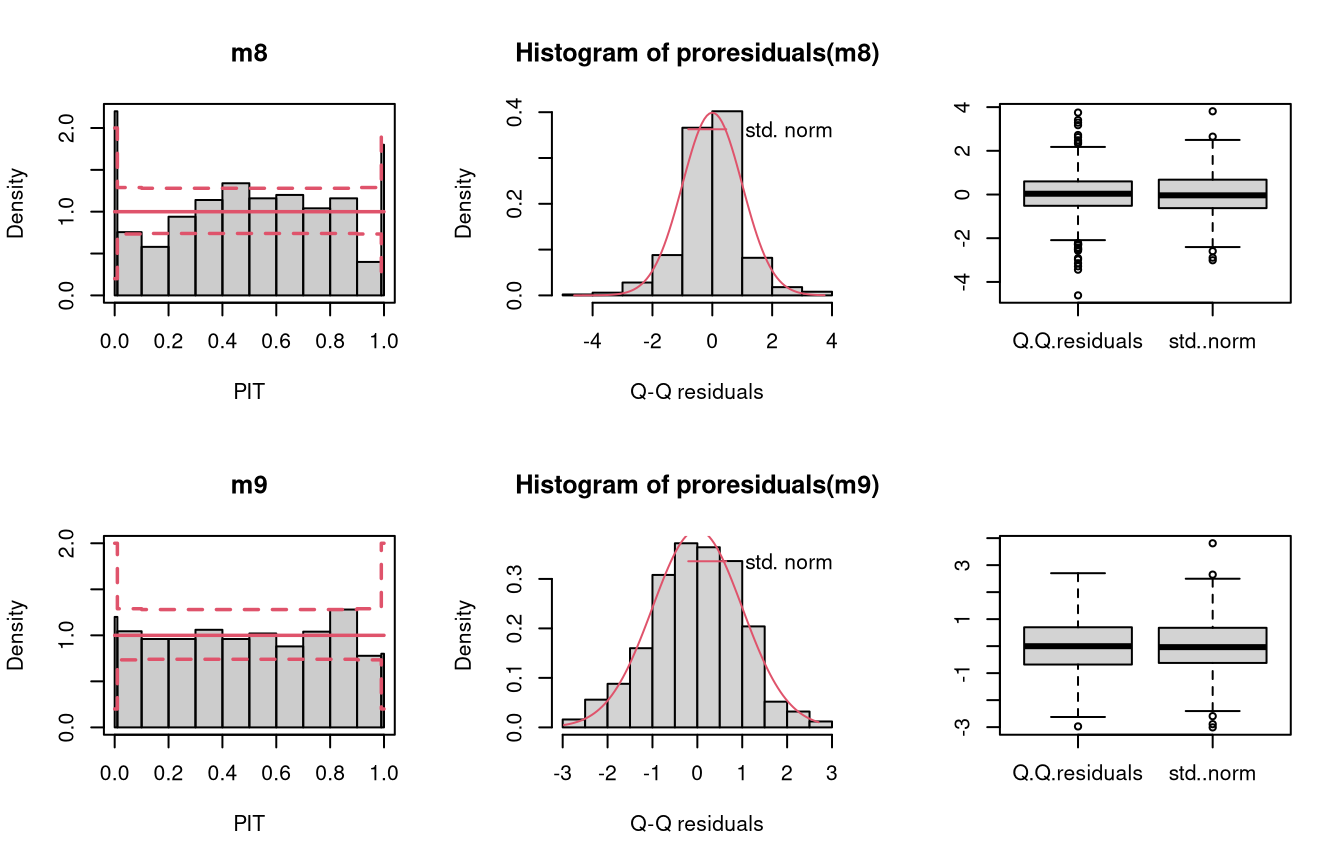
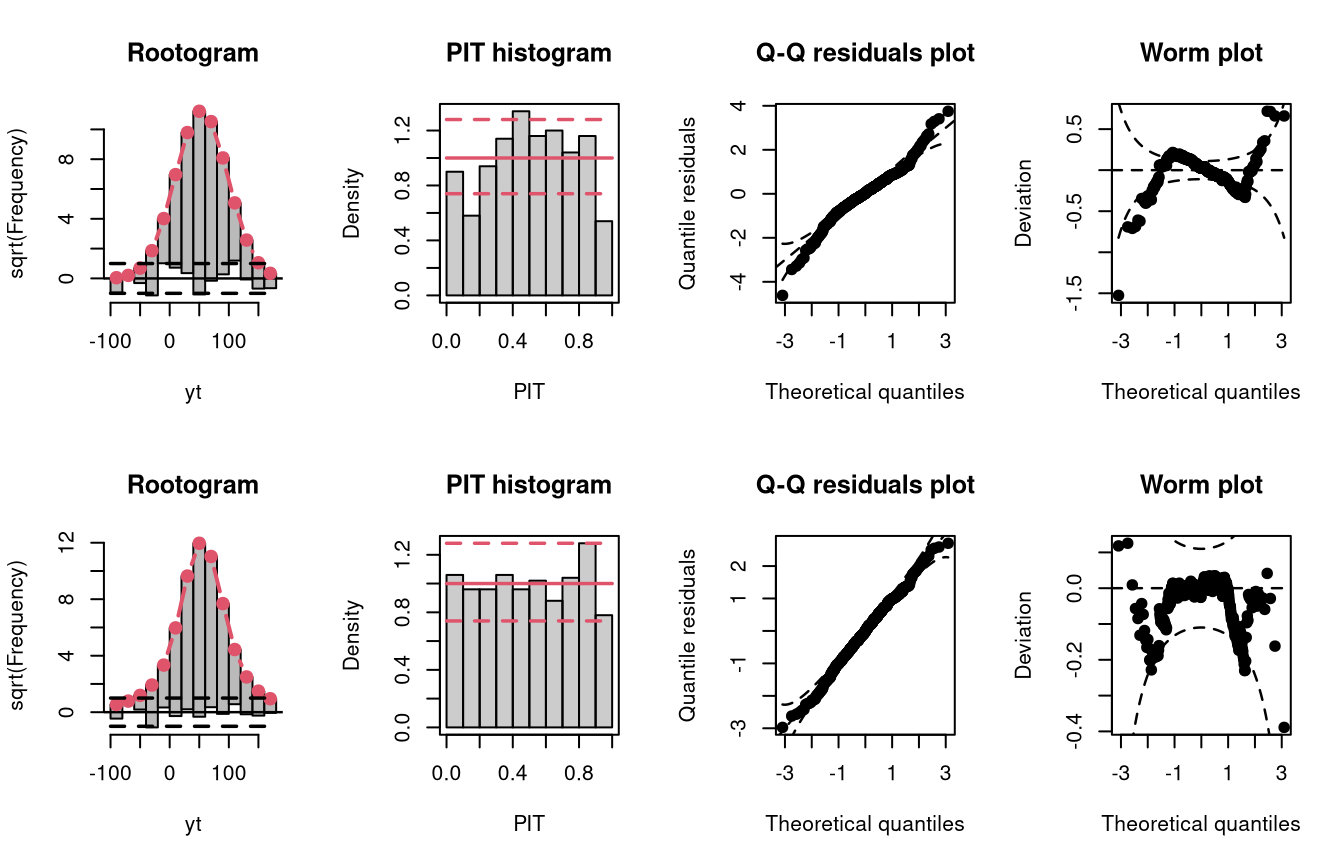
Not accounting for the underlying student-t response distribution (df = 4), which is characterized by heavier tails than the normal distribution, leads to a model fit where the tails of the predictive distribution are to light (compare the previous example with “conditional heteroscedasticity” and the case “tails too light” in the summary plot of Graphical Evaluation: Methodology):
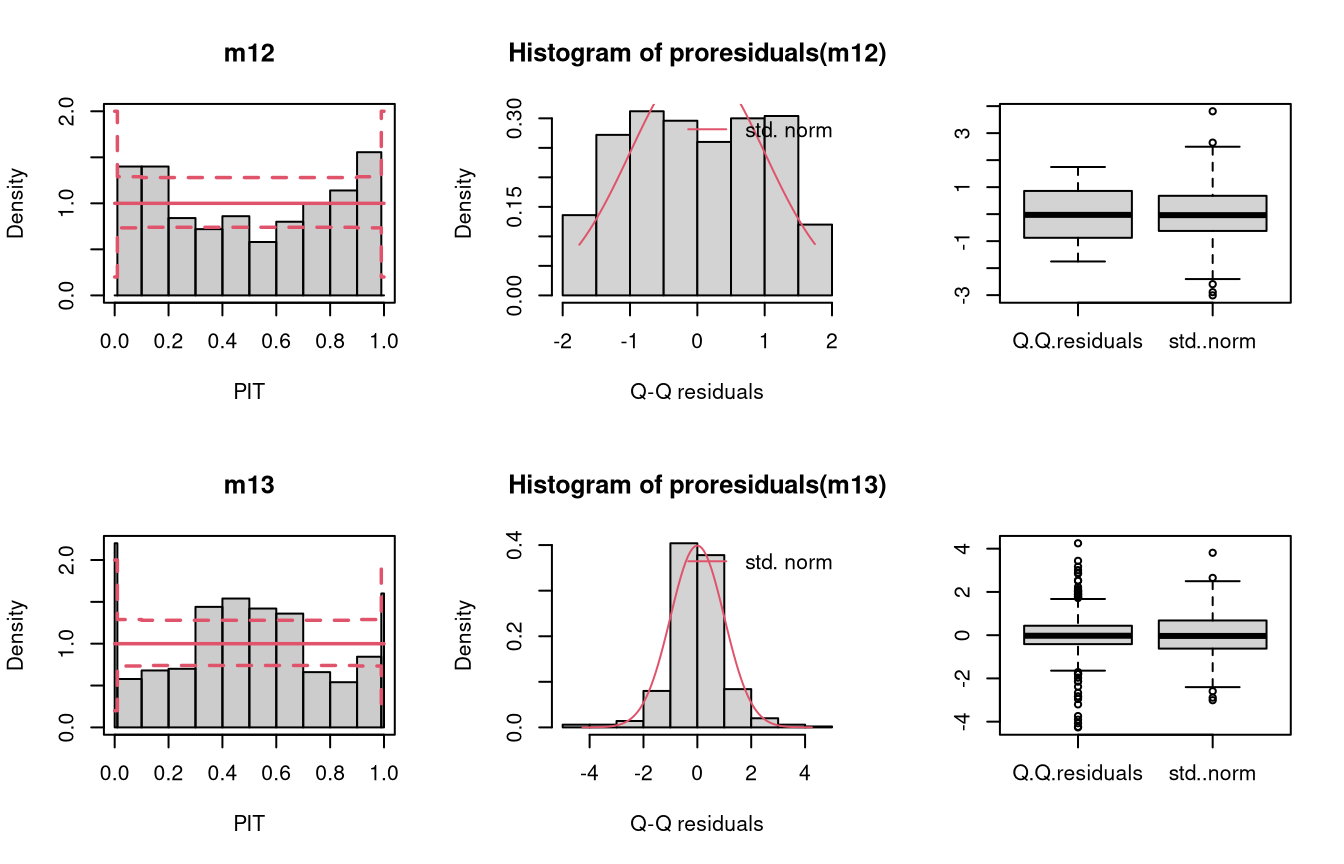
In the example “skewness”, both right-skewed and left-skewed data are simulated, which are not correctly accounted for by the linear models m10 and m11.
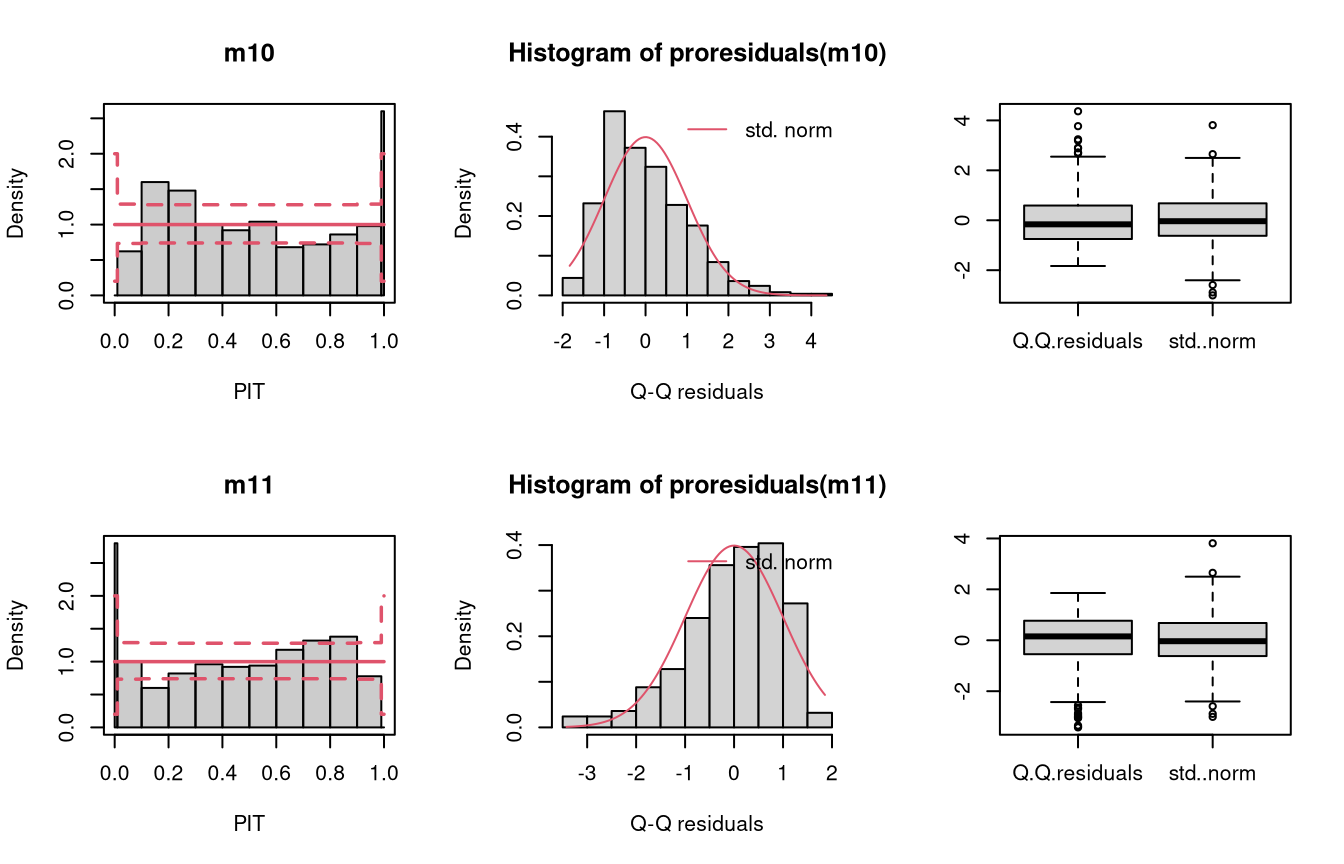
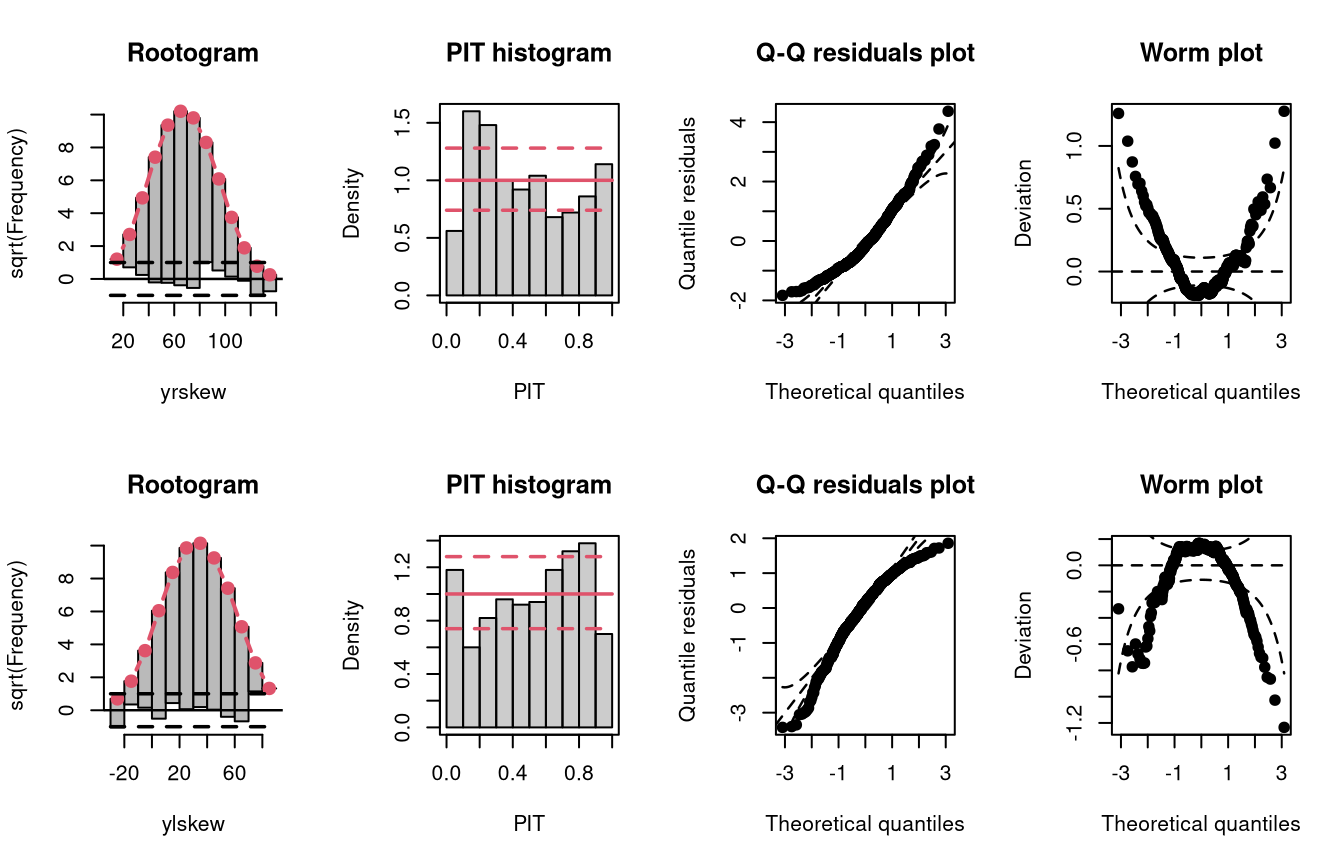
Not accounting for right-skewed or left-skewed data leads to a estimated model with a predictive distribution which is too skewed to the left or right, respectively (compare the cases “too skew to the left/right” in the summary plot of Graphical Evaluation: Methodology):
In the following, two further examples are shown, one with simulated data from a uniform distribution, the second with simulated data from a Laplace distribution. For both data sets, a linear model is estimated without considering the true underlying response distribution.
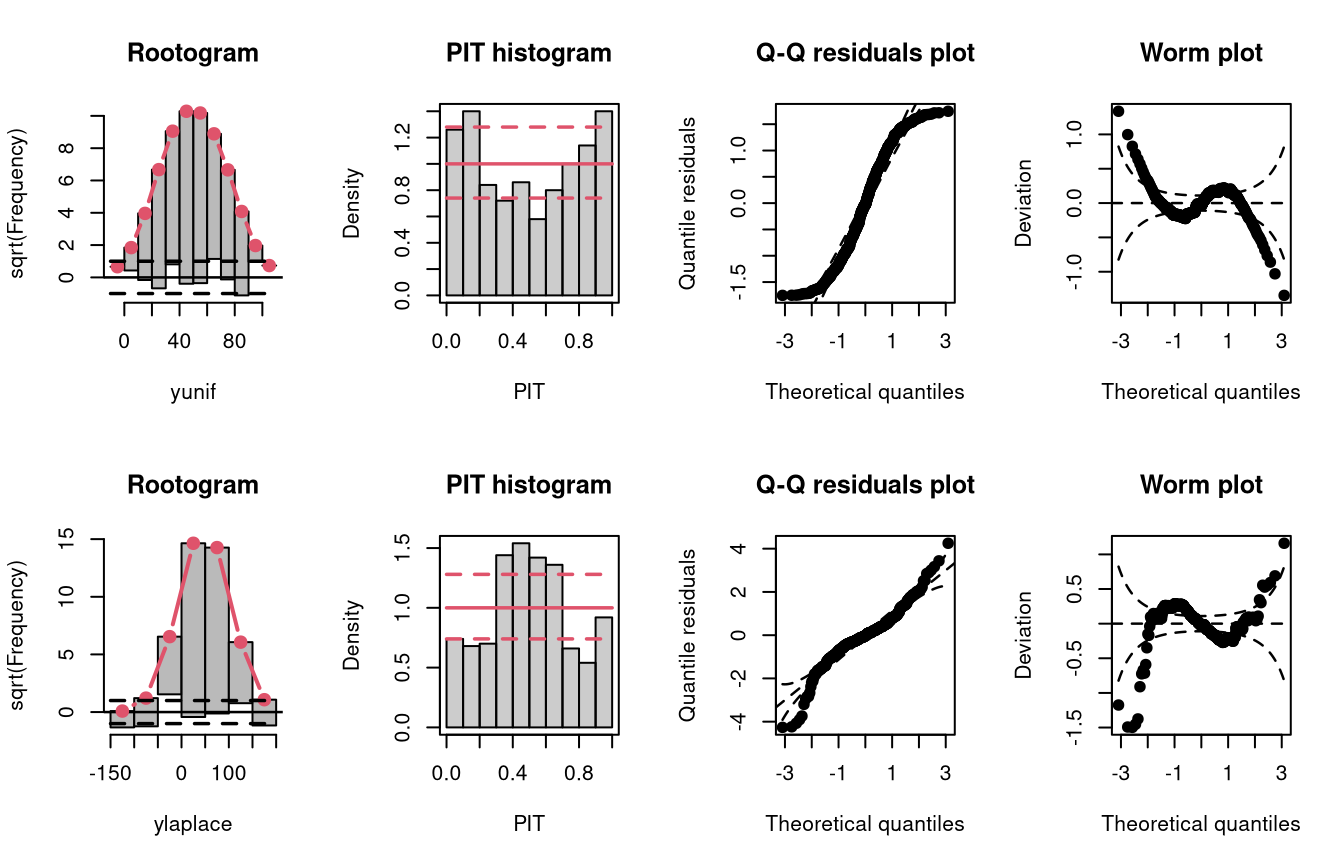
Uniformly distributed data generally have lighter tails than the normal distribution (depending on the lower and upper bounds, of course), while the Laplace distribution here is characterized by heavier tails and a higher probability mass in the center of the distribution than in the normal distribution. Therefore, the uniformly and Laplace distributed data lead to misspecified predictive distributions where the tails are either too heavy or too light, respectively (compare the previous examples “conditional heteroscedasticity” and “Student-t distribution”, where the tails are too light, as well aa the cases “tails too light/heavy” in the summary plot of Graphical Evaluation: Methodology).
Here, uniformly distributed data result in a misspecifed model where the tails of the predictive distribution are too heavy:
Here, Laplace distributed data result in a misspecifed model where the tails of the predictive distribution are too light:
As a reference, first a Poisson model is fitted to Poisson distributed data.
## correct model fit
m14 <- glm(ypois ~ x, data = d, family = poisson)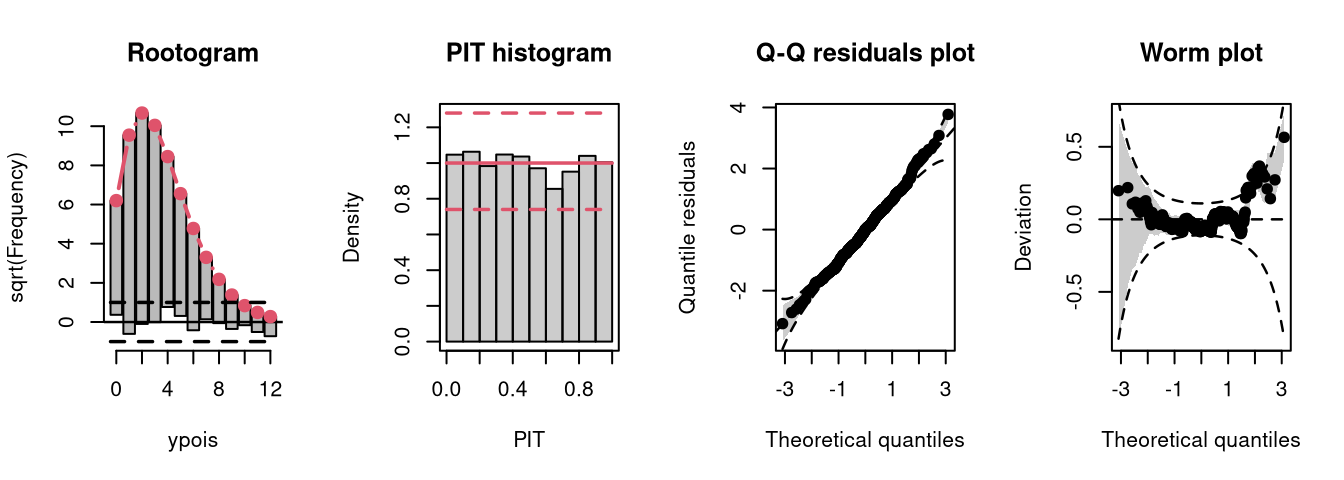
The model fit experiences no misspecifications resulting in a well calibrated predictive distribution (compare the case “well calibrated” in the summary plot of Graphical Evaluation: Methodology):
Two models are fitted to simulated data from a negative binomial distribution. In model m15 an underlying Poisson distribution is incorrectly assumed, in model m16 the negative binomial distribution is correctly accounted for by using glm.nb().
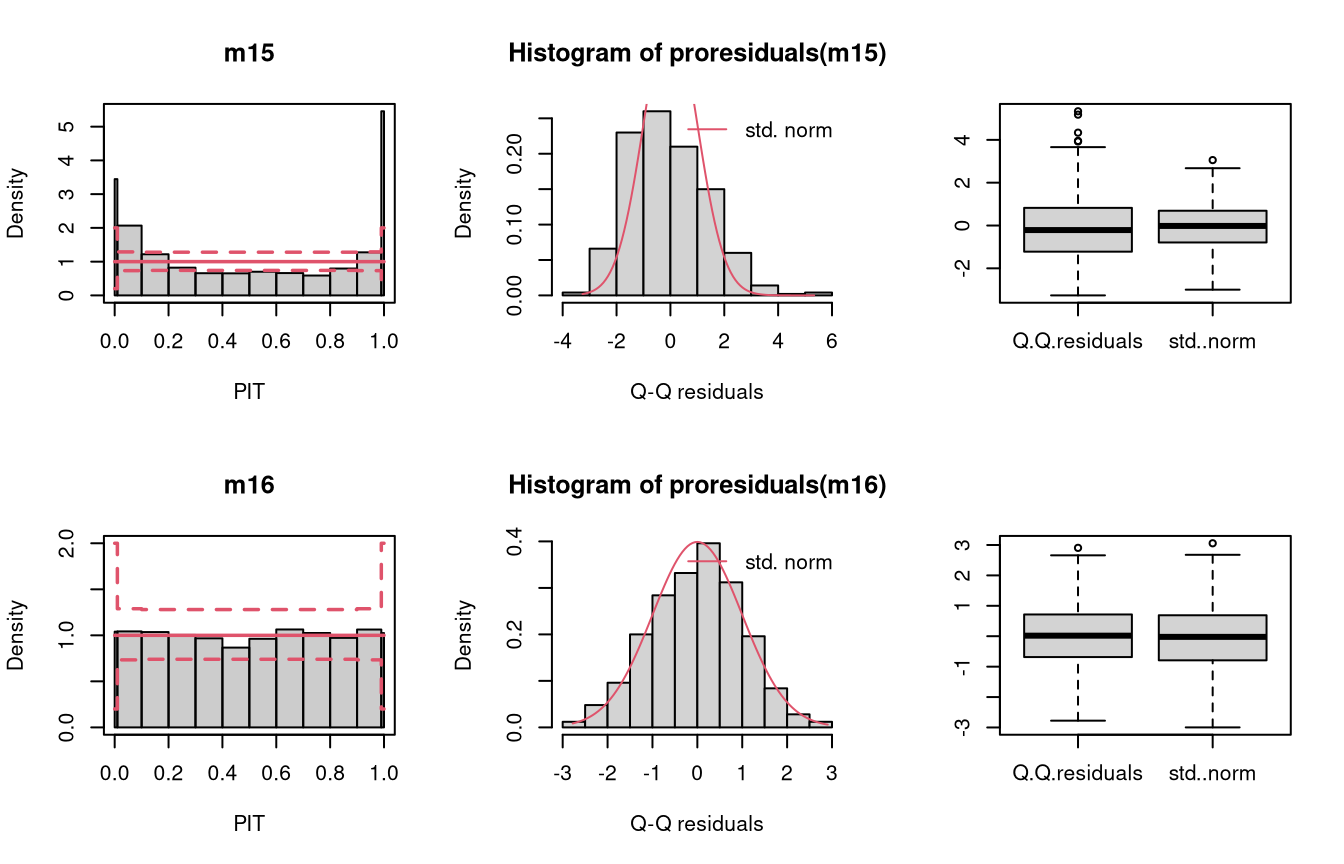
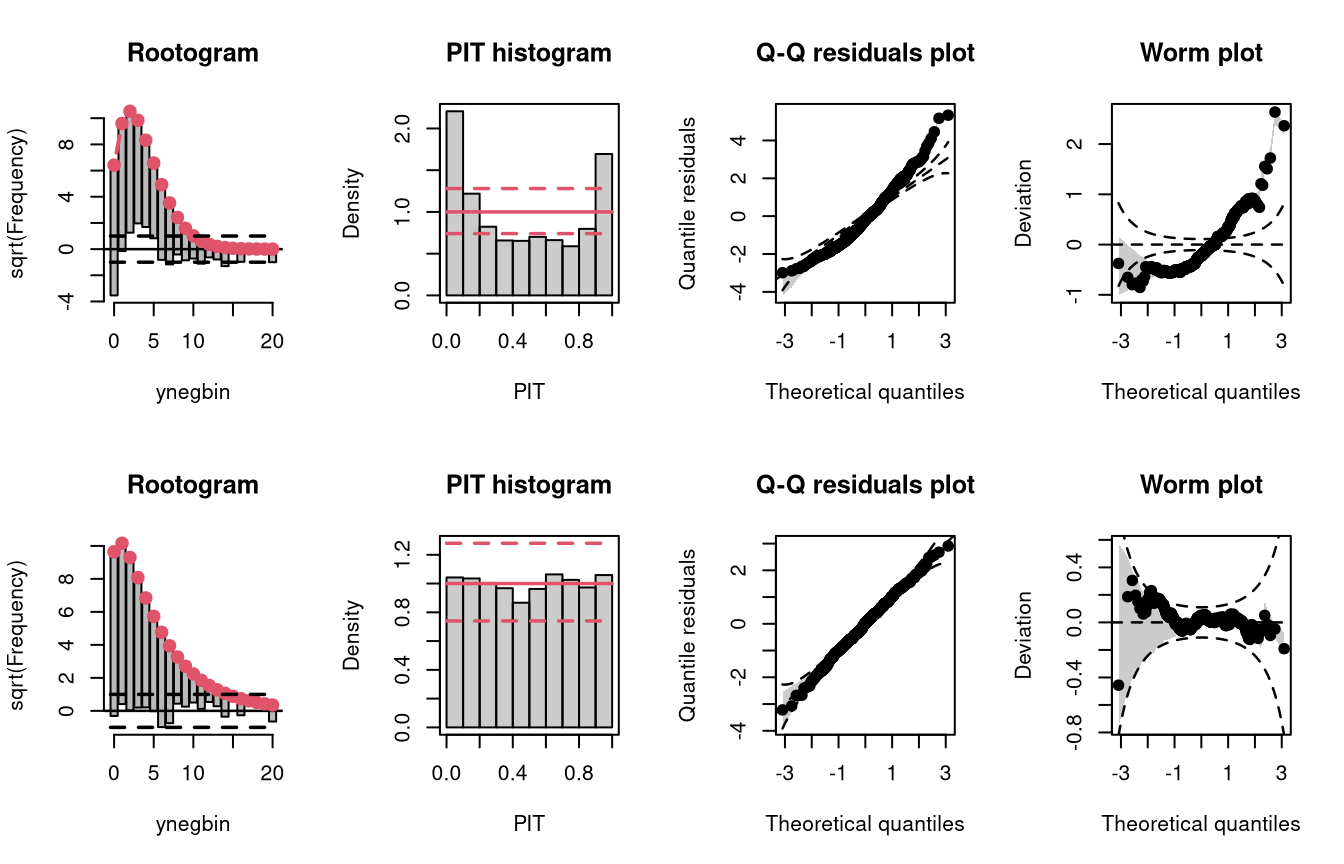
The wrong distribution assumption results in not accounting for the overdispersion in the data, which corresponds to an underdispersed predictive disitriubtion (compare the case “underdispersed” in the summary plot of Graphical Evaluation: Methodology):
Two models are fitted to simulated count data with excess zeros; the model m17 is unable to account for zero inflation, while model m18 fits a zero-inflation regression model that combines a point mass at zero with a Poisson model for higher counts and therefore fits the excess zeros perfectly.
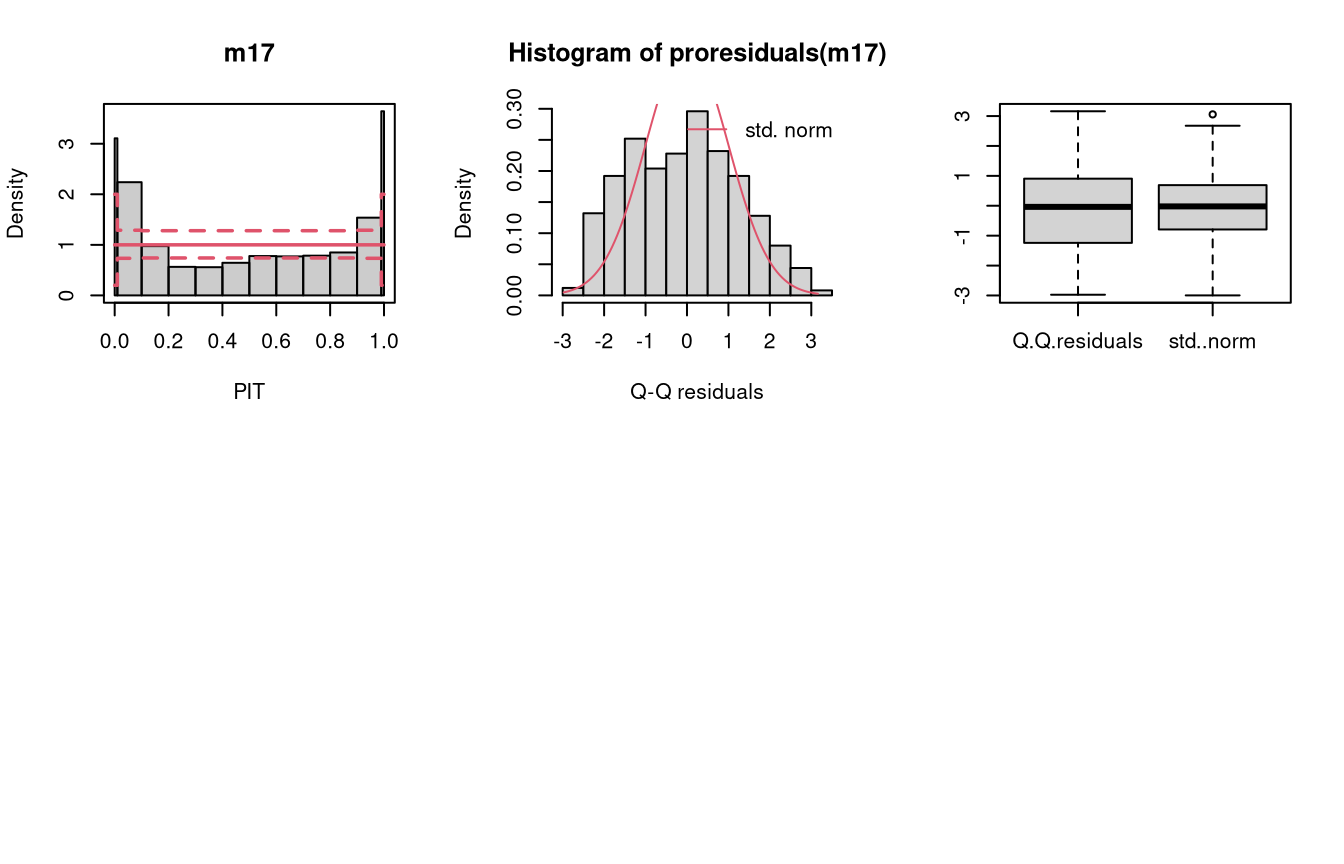
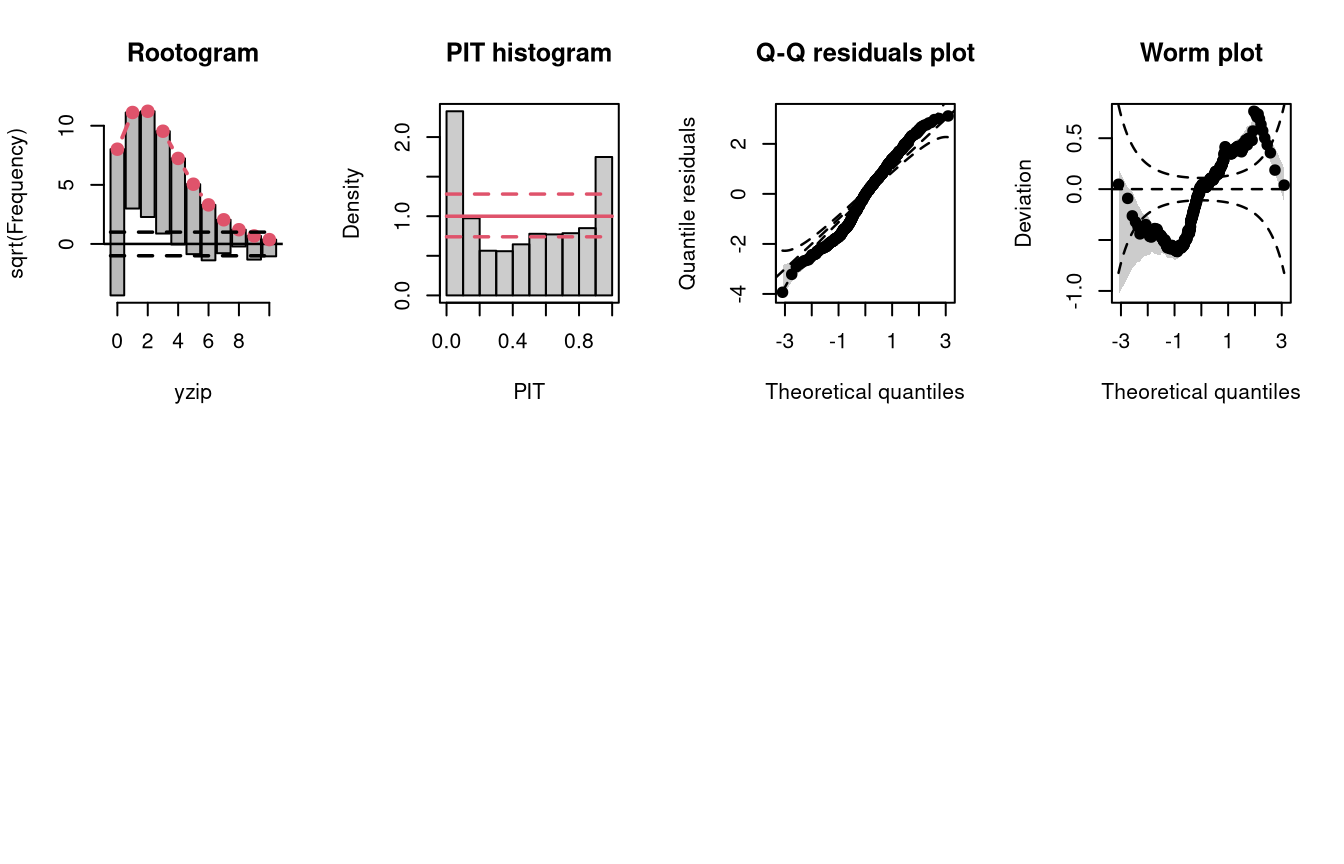
Excess zeros are inevitably linked to overdispersion, so the misspecified model fit without accounting for zero inflation has similar patterns to an underdispersive predictive distribution (compare the previous example with “negative binomial” distributed data and “underdispersed” in the summary plot of Graphical Evaluation: Methodology):